Dabas parādības un procesi mums apkārt ir diezgan sarežģīti. To precīzam fiziskajam aprakstam ir jāizmanto apgrūtinošs matemātiskais aparāts un jāņem vērā liels skaits nozīmīgu faktoru. Lai izvairītos no šīs problēmas, fizikā tiek izmantoti daži vienkāršoti modeļi, kas ievērojami atvieglo procesa matemātisko analīzi, bet praktiski neietekmē tā apraksta precizitāti. Viens no tiem ir ideāls gāzes modelis. Apskatīsim to sīkāk rakstā.
Ideālas gāzes jēdziens
Ideāla gāze ir vielas agregācijas stāvoklis, kas sastāv no materiāliem punktiem, kuri savstarpēji nesadarbojas. Paskaidrosim šo definīciju sīkāk.
Pirmkārt, mēs runājam par materiālajiem punktiem kā objektiem, kas veido ideālu gāzi. Tas nozīmē, ka tā molekulām un atomiem nav izmēra, bet tiem ir noteikta masa. Tas ir drosmīgstuvinājumu var izdarīt, ņemot vērā faktu, ka visās reālajās gāzēs zemā spiedienā un augstā temperatūrā attālums starp molekulām ir daudz lielāks par to lineārajiem izmēriem.
Otrkārt, ideālās gāzes molekulām nevajadzētu mijiedarboties viena ar otru. Patiesībā šāda mijiedarbība pastāv vienmēr. Tātad pat cēlgāzu atomi piedzīvo dipola-dipola pievilcību. Citiem vārdiem sakot, pastāv van der Vāla mijiedarbība. Tomēr, salīdzinot ar molekulu rotācijas un translācijas kustības kinētisko enerģiju, šīs mijiedarbības ir tik mazas, ka neietekmē gāzu īpašības. Tāpēc tos nevar ņemt vērā, risinot praktiskas problēmas.
Ir svarīgi ņemt vērā, ka ne visas gāzes, kurām ir zems blīvums un augsta temperatūra, var uzskatīt par ideālām. Papildus van der Vālsa mijiedarbībai ir arī citi, spēcīgāki saišu veidi, piemēram, ūdeņraža saites starp H2O molekulām, kas izraisa rupju gāzes idealitātes nosacījumu pārkāpumu. Šī iemesla dēļ ūdens tvaiki nav ideāla gāze, bet gaiss ir.
Ideālas gāzes fiziskais modelis
Šo modeli var attēlot šādi: pieņemsim, ka gāzes sistēmā ir N daļiņas. Tie var būt dažādu ķīmisko vielu un elementu atomi un molekulas. N daļiņu skaits ir liels, tāpēc to raksturošanai parasti izmanto vienību "mols" (1 mols atbilst Avogadro skaitlim). Viņi visi pārvietojas kādā tilpumā V. Daļiņu kustībasir haotiski un neatkarīgi viens no otra. Katram no tiem ir noteikts ātrums v un tas pārvietojas pa taisnu ceļu.
Teorētiski daļiņu sadursmes iespējamība ir gandrīz nulle, jo to izmērs ir mazs, salīdzinot ar daļiņu attālumiem. Taču, ja notiek šāda sadursme, tad tā ir absolūti elastīga. Pēdējā gadījumā tiek saglabāts kopējais daļiņu impulss un to kinētiskā enerģija.
Aplūkotais ideālo gāzu modelis ir klasiska sistēma ar milzīgu elementu skaitu. Tāpēc tajā esošo daļiņu ātrums un enerģija pakļaujas Maksvela-Bolcmaņa statistiskajam sadalījumam. Dažām daļiņām ir mazs ātrums, bet citām ir liels ātrums. Šajā gadījumā ir noteikts šaurs ātruma ierobežojums, kurā atrodas šī daudzuma visticamākās vērtības. Zemāk shematiski parādīts slāpekļa molekulu ātruma sadalījums.
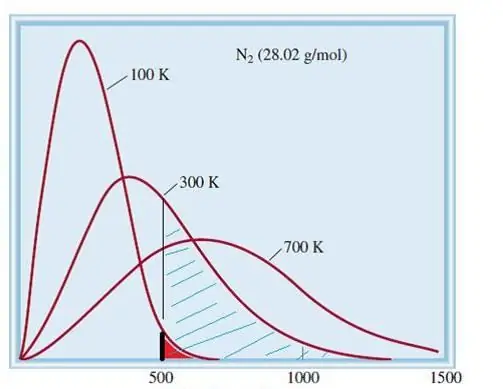
Gāzu kinētiskā teorija
Iepriekš aprakstītais ideālo gāzu modelis unikāli nosaka gāzu īpašības. Šo modeli pirmo reizi ierosināja Daniels Bernulli 1738. gadā.

Vēlāk to līdz pašreizējam stāvoklim izstrādāja Augusts Kroenigs, Rūdolfs Klausiuss, Mihails Lomonosovs, Džeimss Maksvels, Ludvigs Bolcmans, Marians Smoluhovskis un citi zinātnieki.
Šķidruma vielu kinētiskā teorija, uz kuras pamata tiek veidots ideālās gāzes modelis, izskaidro divas svarīgas sistēmas makroskopiskās īpašības, pamatojoties uz tās mikroskopisko uzvedību:
- Spiediens gāzēs ir daļiņu sadursmes ar trauka sienām rezultāts.
- Temperatūra sistēmā ir pastāvīgas molekulu un atomu kustības izpausmes rezultāts.
Izvērsīsim abus kinētiskās teorijas secinājumus.
Gāzes spiediens
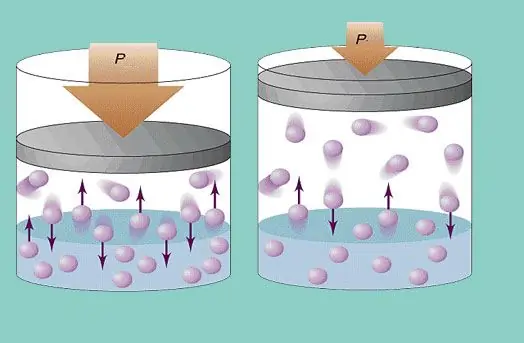
Ideāls gāzes modelis paredz pastāvīgu haotisku daļiņu kustību sistēmā un to pastāvīgu sadursmi ar trauka sienām. Katra šāda sadursme tiek uzskatīta par absolūti elastīgu. Daļiņu masa ir maza (≈10-27-10-25 kg). Tāpēc tas nevar radīt lielu spiedienu sadursmē. Tomēr daļiņu skaits un līdz ar to arī sadursmju skaits ir milzīgs (≈1023). Turklāt elementu vidējais kvadrātiskais ātrums istabas temperatūrā ir vairāki simti metru sekundē. Tas viss rada ievērojamu spiedienu uz kuģa sienām. To var aprēķināt, izmantojot šādu formulu:
P=Nmvcp2 / (3V), kur vcp ir vidējais kvadrātiskais ātrums, m ir daļiņu masa.
Absolūtā temperatūra
Saskaņā ar ideālo gāzes modeli, temperatūru unikāli nosaka molekulas vai atoma vidējā kinētiskā enerģija pētāmajā sistēmā. Varat uzrakstīt šādu izteiksmi, kas saista ideālas gāzes kinētisko enerģiju un absolūto temperatūru:
mvcp2 / 2=3/2kB T.
Šeit kB ir Bolcmaņa konstante. No šīs vienlīdzības mēs iegūstam:
T=m vcp2 / (3kB).
Universālais stāvokļa vienādojums
Ja apvienojam iepriekš minētās izteiksmes absolūtajam spiedienam P un absolūtajai temperatūrai T, mēs varam uzrakstīt šādu vienādību:
PV=nRT.
Šeit n ir vielas daudzums molos, R ir D. I. Mendeļejeva ieviestā gāzes konstante. Šī izteiksme ir vissvarīgākais vienādojums ideālo gāzu teorijā, jo tas apvieno trīs termodinamiskos parametrus (V, P, T) un nav atkarīgs no gāzes sistēmas ķīmiskajām īpašībām.

Universālo vienādojumu 19. gadsimtā pirmo reizi eksperimentāli atvasināja franču fiziķis Emīls Klepeirons, un pēc tam to mūsdienu formā izveidoja krievu ķīmiķis Mendeļejevs, tāpēc pašlaik tajā ir šo zinātnieku vārdi.






