Elastības modulis ir fizikāls lielums, kas raksturo materiāla elastīgo uzvedību, kad tam tiek pielikts ārējs spēks noteiktā virzienā. Materiāla elastība nozīmē tā deformāciju elastīgajā zonā.
Materiālu elastības izpētes vēsture

Elastīgo ķermeņu fizikālo teoriju un to uzvedību ārējo spēku ietekmē detalizēti izskatīja un pētīja 19. gadsimta angļu zinātnieks Tomass Jangs. Taču pašu elastības jēdzienu tālajā 1727. gadā izstrādāja Šveices matemātiķis, fiziķis un filozofs Leonhards Eilers, un pirmie eksperimenti saistībā ar elastības moduli tika veikti 1782. gadā, tas ir, 25 gadus pirms Tomasa Junga darba., Venēcijas matemātiķis un filozofs Jakopo Rikati.
Tomasa Jaga nopelns slēpjas faktā, ka viņš elastības teorijai piešķīra modernu izskatu, kas vēlāk tika formalizēts vienkārša un pēc tam vispārināta Huka likuma formā.
Elastības fiziskā būtība
Jebkurš ķermenis sastāv no atomiem, starp kuriem darbojas pievilkšanas un atgrūšanas spēki. Šo spēku līdzsvars irvielas stāvoklis un parametri noteiktos apstākļos. Cieta ķermeņa atomi, kad tiem tiek pielietoti nenozīmīgi ārējie spriedzes vai saspiešanas spēki, sāk pārvietoties, radot pretēju spēku un vienāda lieluma spēku, kam ir tendence atgriezt atomus sākotnējā stāvoklī.
Šādas atomu pārvietošanas procesā palielinās visas sistēmas enerģija. Eksperimenti liecina, ka pie maziem celmiem enerģija ir proporcionāla šo celmu kvadrātam. Tas nozīmē, ka spēks, kas ir atvasinājums attiecībā pret enerģiju, izrādās proporcionāls celma pirmajai pakāpei, tas ir, tas ir lineāri atkarīgs no tā. Atbildot uz jautājumu, kāds ir elastības modulis, mēs varam teikt, ka tas ir proporcionalitātes koeficients starp spēku, kas iedarbojas uz atomu, un deformāciju, ko šis spēks izraisa. Janga moduļa dimensija ir tāda pati kā spiediena dimensija (Pascal).
Elastīgais ierobežojums
Saskaņā ar definīciju, elastības modulis norāda, cik liels spriegums jāpieliek cietai vielai, lai tās deformācija būtu 100%. Tomēr visām cietajām vielām ir elastības robeža, kas vienāda ar 1% deformāciju. Tas nozīmē, ka, ja tiek pielikts atbilstošs spēks un ķermenis tiek deformēts par mazāk nekā 1%, tad pēc šī spēka pārtraukšanas ķermenis precīzi atjauno savu sākotnējo formu un izmērus. Ja tiek pielikts pārāk liels spēks, pie kura deformācijas vērtība pārsniedz 1%, pēc ārējā spēka pārtraukšanas ķermenis vairs neatjaunos sākotnējos izmērus. Pēdējā gadījumā runā par atlikušās deformācijas esamību, kas irpierādījumi, ka ir pārsniegta materiāla elastības robeža.
Younga modulis darbībā
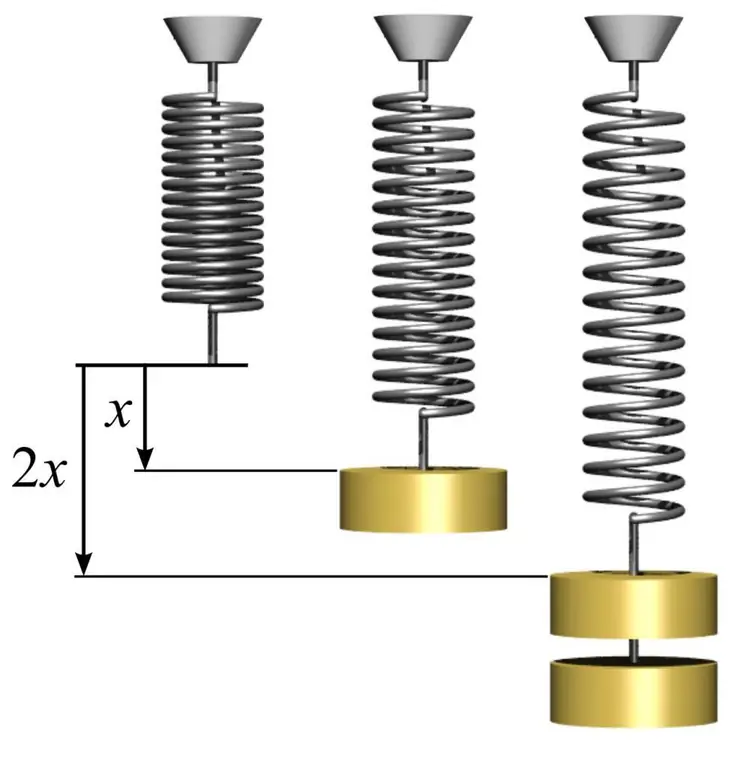
Lai noteiktu elastības moduli, kā arī saprastu, kā to izmantot, varat sniegt vienkāršu piemēru ar atsperi. Lai to izdarītu, jums ir jāņem metāla atspere un jāizmēra apļa laukums, ko veido tās spoles. To veic, izmantojot vienkāršo formulu S=πr², kur n ir pi vienāds ar 3,14 un r ir atsperes spoles rādiuss.
Tālāk izmēriet atsperes garumu l0 bez slodzes. Ja kādu masu m1 uzkarat uz atsperes, tad tā palielinās savu garumu līdz noteiktai vērtībai l1. Elastības moduli E, pamatojoties uz zināšanām par Huka likumu, var aprēķināt pēc formulas: E=m1gl0/(S(l) 1-l0)), kur g ir brīvā kritiena paātrinājums. Šajā gadījumā mēs atzīmējam, ka atsperes deformācijas apjoms elastīgajā reģionā var ievērojami pārsniegt 1%.
Jaga moduļa zināšana ļauj prognozēt deformācijas apjomu noteikta sprieguma iedarbībā. Šajā gadījumā, ja uz atsperes piekarinām citu masu m2, iegūstam šādu relatīvās deformācijas vērtību: d=m2g/ (SE), kur d - relatīvā deformācija elastīgajā reģionā.
Izotropija un anizotropija
Elastības modulis ir materiāla raksturlielums, kas raksturo saites stiprumu starp tā atomiem un molekulām, tomēr konkrētam materiālam var būt vairāki dažādi Jaga moduļi.
Fakts ir tāds, ka katras cietās vielas īpašības ir atkarīgas no tās iekšējās struktūras. Ja īpašības ir vienādas visos telpiskajos virzienos, tad runa ir par izotropisku materiālu. Šādām vielām ir viendabīga struktūra, tāpēc ārēja spēka iedarbība dažādos virzienos uz tām izraisa vienādu materiāla reakciju. Visi amorfie materiāli, piemēram, gumija vai stikls, ir izotropi.
Anizotropija ir parādība, ko raksturo cietas vai šķidruma fizikālo īpašību atkarība no virziena. Visiem metāliem un sakausējumiem uz to bāzes ir viens vai otrs kristāliskais režģis, tas ir, sakārtots, nevis haotisks jonu serdeņu izvietojums. Šādiem materiāliem elastības modulis mainās atkarībā no ārējā sprieguma darbības ass. Piemēram, metāliem ar kubisko simetriju, piemēram, alumīniju, varu, sudrabu, ugunsizturīgiem metāliem un citiem, ir trīs dažādi Janga moduļi.
Bīdes modulis
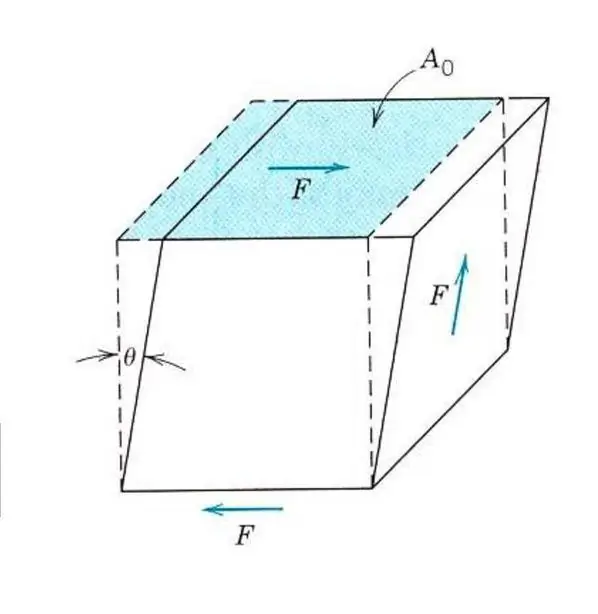
Lai aprakstītu pat izotropa materiāla elastības īpašības, nav vajadzīgas zināšanas par vienu Jangu moduli. Jo papildus spriedzei un saspiešanai materiālu var ietekmēt bīdes spriegumi vai vērpes spriegumi. Šajā gadījumā tas atšķirīgi reaģēs uz ārējo spēku. Lai aprakstītu elastīgo bīdes deformāciju, tiek ieviests Janga moduļa, bīdes moduļa vai otrā veida elastības moduļa analogs.
Visi materiāli iztur bīdes spriegumu, kas ir mazāks par spriegumu vai saspiešanu, tāpēc to bīdes moduļa vērtība ir 2-3 reizes mazāka par Jaga moduļa vērtību. Tādējādi titānam, kura Janga modulis ir vienāds ar 107 GPa, bīdes modulis irtikai 40 GPa, tēraudam šie skaitļi ir attiecīgi 210 GPa un 80 GPa.
Koksnes elastības modulis

Koks ir anizotrops materiāls, jo koksnes šķiedras ir orientētas noteiktā virzienā. Tieši gar šķiedrām tiek mērīts koksnes elastības modulis, jo pāri šķiedrām tas ir par 1-2 kārtām mazāks. Zināšanas par Janga moduli koksnei ir svarīgas, un tās tiek ņemtas vērā, projektējot koka paneļu konstrukcijas.
Koksnes elastības moduļa vērtības dažiem koku veidiem ir parādītas zemāk esošajā tabulā.
| Koka skats | Junga modulis GPa |
| Lauru koks | 14 |
| Eucalyptus | 18 |
| Ciedrs | 8 |
| Egle | 11 |
| Pride | 10 |
| Ozols | 12 |
Jāatzīmē, ka norādītās vērtības konkrētam kokam var atšķirties līdz pat 1 GPa, jo tā Jangsa moduli ietekmē koksnes blīvums un augšanas apstākļi.

Bīdes moduļi dažādām koku sugām ir robežās no 1-2 GPa, piemēram, priedei tas ir 1,21 GPa, bet ozolam 1,38 GPa, tas ir, koksne praktiski neiztur bīdes spriegumus. Šis fakts ir jāņem vērā, ražojot koka nesošās konstrukcijas, kas paredzētas darbam tikai nospriegojumā vai spiedienā.
Metālu elastīgās īpašības
Salīdzinot ar Janga koksnes moduli, šīs vērtības vidējās vērtības metāliem un sakausējumiem ir par vienu pakāpi lielākas, kā parādīts nākamajā tabulā.
| Metāls | Junga modulis GPa |
| Bronza | 120 |
| Varš | 110 |
| Tērauds | 210 |
| Titāns | 107 |
| Niķelis | 204 |
Metālu, kuriem ir kubiskā singonija, elastīgās īpašības raksturo trīs elastīgās konstantes. Pie šādiem metāliem pieder varš, niķelis, alumīnijs, dzelzs. Ja metālam ir sešstūra singonija, tad jau ir vajadzīgas sešas konstantes, lai aprakstītu tā elastības raksturlielumus.
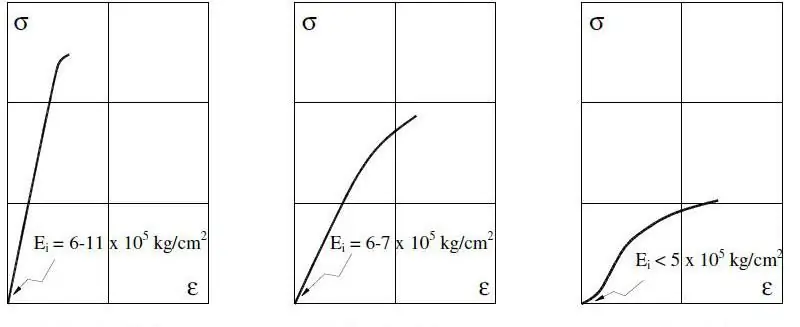
Metāliskām sistēmām Janga modulis tiek mērīts 0,2% deformācijas robežās, jo neelastīgajā reģionā jau var rasties lielas vērtības.






