Kā jūs zināt, jebkurš fiziskais lielums pieder vienam no diviem veidiem, tas ir vai nu skalārs, vai vektors. Šajā rakstā mēs aplūkosim tādas kinemātiskās īpašības kā ātrums un paātrinājums, kā arī parādīsim, kur ir vērsti paātrinājuma un ātruma vektori.
Kas ir ātrums un paātrinājums?
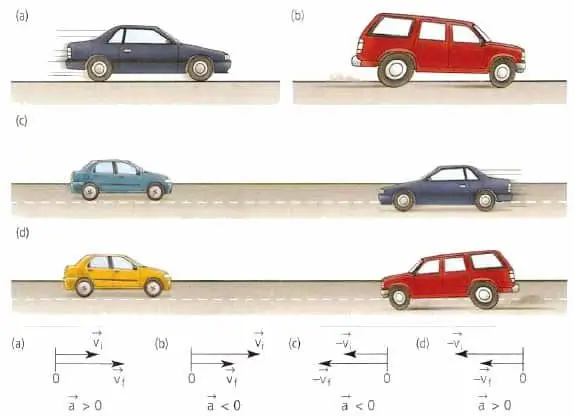
Abi šajā punktā minētie lielumi ir jebkura veida kustības svarīgas īpašības neatkarīgi no tā, vai tā pārvieto ķermeni pa taisnu līniju vai pa izliektu ceļu.
Ātrums ir ātrums, ar kādu laika gaitā mainās koordinātas. Matemātiski šī vērtība ir vienāda ar nobrauktā attāluma laika atvasinājumu, tas ir:
v¯=dl¯/dt.
Šeit vektors l¯ ir vērsts no ceļa sākuma punkta uz beigu punktu.
Savukārt paātrinājums ir ātrums, ar kādu pats ātrums mainās laikā. Formulas veidā to var uzrakstīt šādi:
a¯=dv¯/dt.
Acīmredzot, ņemot otro atvasinājumu nonobīdes vektors l¯ laikā, mēs iegūsim arī paātrinājuma vērtību.
Tā kā ātrumu mēra metros sekundē, paātrinājums saskaņā ar rakstīto izteiksmi tiek mērīts metros sekundē kvadrātā.

Kur ir paātrinājuma un ātruma vektori?
Fizikā jebkurai ķermeņa mehāniskai kustībai parasti ir raksturīga noteikta trajektorija. Pēdējais ir kaut kāda iedomāta līkne, pa kuru ķermenis pārvietojas telpā. Piemēram, taisna līnija vai aplis ir galvenie parasto kustības ceļu piemēri.
Ķermeņa ātruma vektors vienmēr ir vērsts kustības virzienā, neatkarīgi no tā, vai ķermenis palēninās vai paātrinās, vai tas kustas taisnā līnijā vai pa līkumu. Runājot ģeometriski, ātruma vektors ir vērsts tangenciāli uz trajektorijas punktu, kurā pašlaik atrodas ķermenis.
Materiāla vai ķermeņa punkta paātrinājuma vektoram nav nekā kopīga ar ātrumu. Šis vektors ir vērsts ātruma maiņas virzienā. Piemēram, taisnvirziena kustībai vērtība a¯ var vai nu sakrist virzienā ar v¯ vai būt pretēja v¯.
Spēks, kas iedarbojas uz ķermeni un paātrinājums
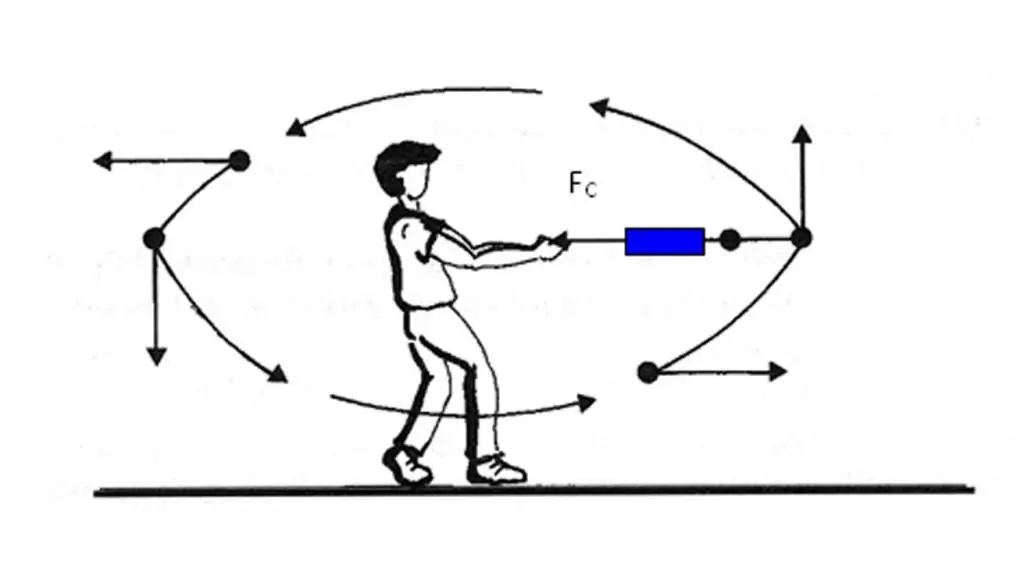
Esam noskaidrojuši, ka ķermeņa paātrinājuma vektors ir vērsts uz ātruma vektora maiņu. Tomēr ne vienmēr ir viegli noteikt, kā mainās ātrums noteiktā trajektorijas punktā. Turklāt, lai noteiktu ātruma izmaiņas, ir jāveic operācijavektoru atšķirības. Lai izvairītos no šīm grūtībām, nosakot vektora a¯ virzienu, ir vēl viens veids, kā ātri noskaidrot.
Zemāk ir slavenais un katram studentam labi zināms Ņūtona likums:
F¯=ma¯.
Formula parāda, ka ķermeņu paātrinājuma cēlonis ir spēks, kas uz tiem iedarbojas. Tā kā masa m ir skalārs, spēka vektors F¯ un paātrinājuma vektors a¯ atrodas vienā virzienā. Šis fakts ir jāatceras un jāpiemēro praksē ikreiz, kad ir nepieciešams noteikt daudzuma virzienu a¯.
Ja uz ķermeni iedarbojas vairāki dažādi spēki, tad paātrinājuma vektora virziens būs vienāds ar visu spēku iegūto vektoru.
Apļveida kustība un paātrinājums
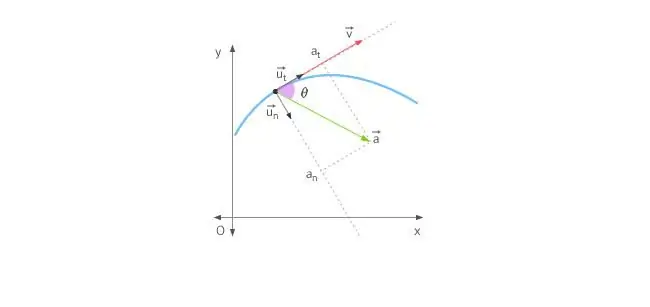
Kad ķermenis pārvietojas taisnā līnijā, paātrinājums tiek virzīts uz priekšu vai atpakaļ. Kustības gadījumā pa apli situāciju sarežģī fakts, ka ātruma vektors nepārtraukti maina savu virzienu. Ņemot vērā iepriekš minēto, kopējo paātrinājumu nosaka divas tā sastāvdaļas: tangenciālais un parastais paātrinājums.
Tangenciālais paātrinājums ir vērsts tieši tāpat kā ātruma vektors vai pret to. Citiem vārdiem sakot, šī paātrinājuma sastāvdaļa ir vērsta gar trajektorijas pieskari. Tangenciālais paātrinājums raksturo paša ātruma moduļa izmaiņas.
Normāls paātrinājums tiek virzīts pa normālu uz doto trajektorijas punktu, ņemot vērā tā izliekumu. Apļveida kustības gadījumā šīs sastāvdaļas vektors norādauz centru, tas ir, parastais paātrinājums ir vērsts pa griešanās rādiusu. Šo komponentu bieži sauc par centripetālu.
Pilns paātrinājums ir šo komponentu summa, tāpēc tā vektoru var patvaļīgi novirzīt attiecībā pret riņķa līniju.
Ja ķermenis griežas, nemainot lineāro ātrumu, tad ir tikai normāls komponents, kas nav nulle, tātad pilnais paātrinājuma vektors ir vērsts uz apļa centru. Ņemiet vērā, ka šo centru ietekmē arī spēks, kas notur ķermeni savā trajektorijā. Piemēram, Saules gravitācijas spēks notur mūsu Zemi un citas planētas savās orbītās.






