Mūsu šodienas raksta tēma būs materiāla punkta kinemātika. Par ko ir runa? Kādi jēdzieni tajā parādās un kāda definīcija būtu jāpiešķir šim terminam? Mēs šodien centīsimies atbildēt uz šiem un daudziem citiem jautājumiem.
Definīcija un jēdziens
Materiālā punkta kinemātika ir nekas vairāk kā fizikas apakšnodaļa, ko sauc par "mehāniku". Viņa savukārt pēta noteiktu ķermeņu kustības modeļus. Materiālā punkta kinemātika arī risina šo problēmu, bet nedara to vispārīgā veidā. Faktiski šajā apakšnodaļā tiek pētītas metodes, kas ļauj aprakstīt ķermeņu kustību. Šajā gadījumā pētījumiem ir piemēroti tikai tā sauktie idealizētie ķermeņi. Tajos ietilpst: materiālais punkts, absolūti stingrs ķermenis un ideāla gāze. Apskatīsim jēdzienus sīkāk. Mēs visi no skolas sola zinām, ka par materiālu punktu pieņemts saukt ķermeni, kura izmērus konkrētā situācijā var atstāt novārtā. Starp citu, pirmo reizi sākas materiāla punkta translācijas kustības kinemātikaparādās septītās klases fizikas mācību grāmatās. Šī ir vienkāršākā nozare, tāpēc ar tās palīdzību visērtāk ir uzsākt iepazīšanos ar zinātni. Atsevišķs jautājums ir par to, kādi ir materiāla punkta kinemātikas elementi. To ir diezgan daudz, un nosacīti tos izpratnei var iedalīt vairākos līmeņos ar dažādu sarežģītību. Ja mēs runājam, piemēram, par rādiusa vektoru, tad principā tā definīcijā nav nekā pārmērīgi sarežģīta. Tomēr piekritīsiet, ka skolēnam to saprast būs daudz vieglāk nekā vidusskolas vai vidusskolas skolēnam. Un, godīgi sakot, šī termina iezīmes vidusskolēniem nav jāskaidro.
Īsa kinemātikas radīšanas vēsture
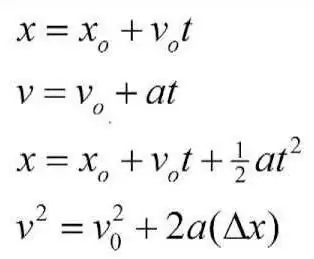
Pirms daudziem, daudziem gadiem izcilais zinātnieks Aristotelis lauvas tiesu no sava brīvā laika veltīja fizikas kā atsevišķas zinātnes izpētei un aprakstam. Viņš strādāja arī pie kinemātikas, mēģinot izklāstīt tās galvenās tēzes un jēdzienus, kas vienā vai otrā veidā tiek izmantoti praktisku un pat ikdienas problēmu risināšanā. Aristotelis sniedza sākotnējās idejas par to, kas ir materiāla punkta kinemātikas elementi. Viņa darbi un darbi ir ļoti vērtīgi visai cilvēcei. Tomēr savos secinājumos viņš pieļāva ievērojamu skaitu kļūdu, un iemesls tam bija daži maldīgi priekšstati un nepareizi aprēķini. Savulaik par Aristoteļa darbiem interesējās cits zinātnieks Galilejs Galilejs. Viena no Aristoteļa pamattēzēm bija tāda, ka ķermeņa kustībanotiek tikai tad, ja uz to iedarbojas kāds spēks, ko nosaka intensitāte un virziens. Galileo pierādīja, ka tā bija kļūda. Spēks ietekmēs kustības ātruma parametru, bet ne vairāk. Itālis parādīja, ka spēks ir paātrinājuma cēlonis, un tas var rasties tikai abpusēji ar to. Tāpat Galileo Galilejs lielu uzmanību pievērsa brīvā kritiena procesa izpētei, atvasinot atbilstošus modeļus. Droši vien visi atceras viņa slavenos eksperimentus, ko viņš veica Pizas tornī. Fiziķis Ampērs savos darbos izmantoja arī kinemātisko risinājumu pamatus.
Sākotnējie jēdzieni
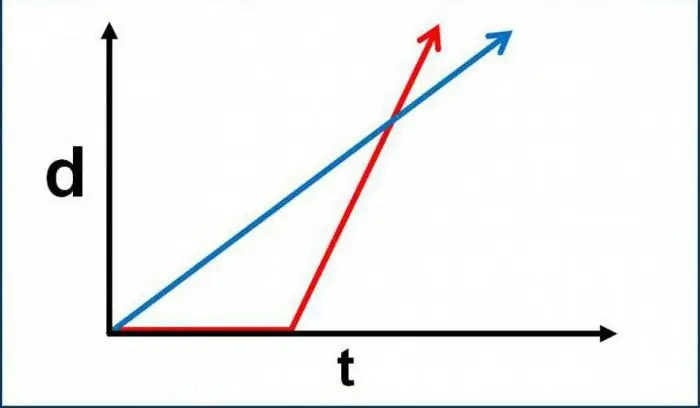
Kā minēts iepriekš, kinemātika ir pētījums par veidiem, kā aprakstīt idealizētu objektu kustību. Šajā gadījumā praksē var pielietot matemātiskās analīzes pamatus, parasto algebru un ģeometriju. Bet kādi jēdzieni (precīzi jēdzieni, nevis parametru lielumu definīcijas) ir šīs fizikas apakšnodaļas pamatā? Pirmkārt, ikvienam ir skaidri jāsaprot, ka materiāla punkta translācijas kustības kinemātika ņem vērā kustību, neņemot vērā spēka rādītājus. Tas ir, lai atrisinātu atbilstošās problēmas, mums nav vajadzīgas formulas, kas saistītas ar spēku. To neņem vērā kinemātika, lai cik viņu būtu - viens, divi, trīs, vismaz vairāki simti tūkstošu. Neskatoties uz to, paātrinājuma esamība joprojām tiek nodrošināta. Vairākās problēmās materiāla punkta kustības kinemātika paredz noteikt paātrinājuma lielumu. Tomēr šīs parādības cēloņi (tas ir, spēki unto raksturs) netiek ņemti vērā, bet gan izlaisti.
Klasifikācija
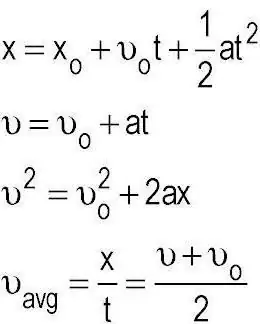
Mēs noskaidrojām, ka kinemātika pēta un izmanto metodes, lai aprakstītu ķermeņu kustību, neņemot vērā spēkus, kas uz tiem iedarbojas. Starp citu, ar šādu uzdevumu nodarbojas cita mehānikas apakšnodaļa, ko sauc par dinamiku. Jau tur tiek piemēroti Ņūtona likumi, kas praksē ļauj noteikt diezgan daudz parametru ar nelielu zināmu sākotnējo datu apjomu. Materiālā punkta kinemātikas pamatjēdzieni ir telpa un laiks. Un saistībā ar zinātnes attīstību gan kopumā, gan šajā jomā radās jautājums par šādas kombinācijas izmantošanas lietderību.
No paša sākuma bija klasiskā kinemātika. Var teikt, ka to raksturo ne tikai gan laika, gan telpisku spraugu klātbūtne, bet arī to neatkarība no viena vai otra atskaites sistēmas izvēles. Starp citu, mēs par to runāsim nedaudz vēlāk. Tagad tikai paskaidrosim, par ko mēs runājam. Šajā gadījumā segments tiks uzskatīts par telpisko intervālu, un laika intervāls tiks uzskatīts par laika intervālu. Šķiet, ka viss ir skaidrs. Tātad šīs nepilnības klasiskajā kinemātikā tiks uzskatītas par absolūtām, nemainīgām, citiem vārdiem sakot, neatkarīgi no pārejas no viena atskaites sistēmas uz otru. Vai biznesa relativistiskā kinemātika. Tajā var mainīties spraugas pārejas laikā starp atskaites sistēmām. Pat pareizāk būtu teikt, ka nevar, bet droši vien ir. Sakarā ar to abu vienlaicīgumsnejauši notikumi arī kļūst relatīvi un tiek pakļauti īpašai uzmanībai. Tāpēc relativistiskajā kinemātikā divi jēdzieni - telpa un laiks - tiek apvienoti vienā.
Materiāla punkta kinemātika: ātrums, paātrinājums un citi lielumi
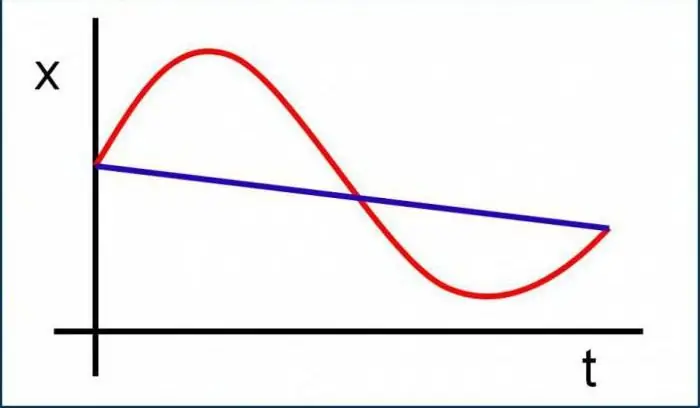
Lai kaut nedaudz izprastu šo fizikas apakšnodaļu, ir jāorientējas svarīgākajos jēdzienos, jāzina definīcijas un jāiedomājas, kas vispār ir tas vai cits daudzums. Šajā nav nekā sarežģīta, patiesībā viss ir ļoti viegli un vienkārši. Iespējams, sākumā apsveriet kinemātikas problēmās izmantotos pamatjēdzienus.
Kustība
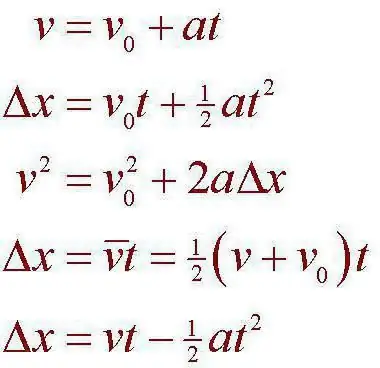
Mehānisko kustību aplūkosim procesu, kura laikā viens vai otrs idealizēts objekts maina savu pozīciju telpā. Šajā gadījumā mēs varam teikt, ka izmaiņas notiek attiecībā pret citiem ķermeņiem. Jāņem vērā arī tas, ka noteikta laika intervāla noteikšana starp diviem notikumiem notiek vienlaicīgi. Piemēram, būs iespējams izolēt noteiktu intervālu, kas veidojas laikā, kas pagājis starp ķermeņa nokļūšanu no vienas pozīcijas uz otru. Mēs arī atzīmējam, ka šajā gadījumā ķermeņi var mijiedarboties viens ar otru saskaņā ar vispārējiem mehānikas likumiem. Tieši ar to visbiežāk darbojas materiāla punkta kinemātika. Atsauces sistēma ir nākamais jēdziens, kas ar to ir nesaraujami saistīts.
Koordinātas
Tos var saukt par parastiem datiem, kas ļauj noteikt ķermeņa stāvokli vienā vai otrā reizē. Koordinātas ir nesaraujami saistītas ar atskaites sistēmas jēdzienu, kā arī koordinātu režģi. Visbiežāk tās ir burtu un ciparu kombinācijas.
Rādiusa vektors
No nosaukuma jau vajadzētu saprast, kas tas ir. Tomēr parunāsim par to sīkāk. Ja punkts pārvietojas pa noteiktu trajektoriju un mēs precīzi zinām noteiktas atskaites sistēmas sākumu, tad mēs jebkurā laikā varam uzzīmēt rādiusa vektoru. Tas savienos punkta sākotnējo pozīciju ar momentāno vai galīgo pozīciju.
Trajektorija
Tā tiks saukta par nepārtrauktu līniju, kas tiek noteikta materiāla punkta kustības rezultātā noteiktā atskaites sistēmā.
Ātrums (gan lineārs, gan leņķiskais)
Šī ir vērtība, kas var noteikt, cik ātri ķermenis veic noteiktu attāluma intervālu.
Paātrinājums (gan leņķiskais, gan lineārs)
Rāda, pēc kāda likuma un cik intensīvi mainās ķermeņa ātruma parametrs.
Varbūt, lūk, tie ir - materiāla punkta kinemātikas galvenie elementi. Jāņem vērā, ka gan ātrums, gan paātrinājums ir vektora lielumi. Un tas nozīmē, ka tiem ir ne tikai kāda orientējoša vērtība, bet arī noteikts virziens. Starp citu, tos var virzīt gan vienā virzienā, gan pretējos virzienos. Pirmajā gadījumā ķermenis paātrinās, otrajā - palēnināsies.
Vienkārši uzdevumi
Materiālā punkta kinemātika (ātrums, paātrinājums un attālums, kuros praktiski ir pamatjēdzieni) ietver ne tikai milzīgu uzdevumu skaitu, bet arī daudzas to dažādās kategorijas. Mēģināsim atrisināt diezgan vienkāršu uzdevumu, nosakot ķermeņa nobraukto attālumu.
Pieņemsim, ka mūsu rīcībā esošie nosacījumi ir šādi. Vadītāja automašīna atrodas uz starta līnijas. Operators ar karogu dod atļauju, un automašīna pēkšņi paceļas. Noskaidro, vai viņa var uzstādīt jaunu rekordu braucēju konkurencē, ja nākamā līdere simts metru distanci veica 7,8 sekundēs. Ņemiet automašīnas paātrinājumu, kas vienāds ar 3 metriem, dalītu ar sekundi kvadrātā.
Tātad, kā atrisināt šo problēmu? Tas ir diezgan interesanti, jo mums tiek prasīts "neizžūt" noteikt noteiktus parametrus. To paspilgtina apgrozījumi un noteikta situācija, kas dažādo rādītāju risināšanas un meklēšanas procesu. Bet pēc kā mums būtu jāvadās pirms uzdevuma veikšanas?
1. Materiālā punkta kinemātika šajā gadījumā paredz paātrinājuma izmantošanu.
2. Risinājums tiek pieņemts, izmantojot attāluma formulu, jo tā skaitliskā vērtība parādās nosacījumos.
Problēma faktiski ir atrisināta pavisam vienkārši. Lai to izdarītu, mēs ņemam attāluma formulu: S=VoT + (-) AT ^ 2/2. Kāda jēga? Mums ir jānoskaidro, cik ilgi braucējs veiks noteikto distanci, un tad jāsalīdzina skaitlis ar rekordu, lai noskaidrotu, vai viņš to pārspēj vai nē. Lai to izdarītu, piešķiriet laiku, iegūstam formuluviņam: AT^2 + 2VoT - 2S. Tas nav nekas vairāk kā kvadrātvienādojums. Bet auto paceļas, kas nozīmē, ka sākotnējais ātrums būs 0. Atrisinot vienādojumu, diskriminants būs vienāds ar 2400. Lai atrastu laiku, ir jāieņem sakne. Izdarīsim to līdz otrajai zīmei aiz komata: 48,98. Atrodiet vienādojuma sakni: 48,98/6=8,16 sekundes. Izrādās, ka šoferim neizdosies pārspēt esošo rekordu.






