Gāzes no termodinamikas viedokļa raksturo makroskopisko raksturlielumu kopums, no kuriem galvenie ir temperatūra, spiediens un tilpums. Viena no šiem parametriem nemainīgums un pārējo divu izmaiņas liecina, ka gāzē notiek viens vai otrs izoprocess. Mēs šo rakstu veltīsim detalizētai atbildei uz jautājumiem, ka šis ir izohorisks process, kā tas atšķiras no izotermiskām un izobariskām izmaiņām gāzes sistēmas stāvokļos.
Ideāla gāze fizikā

Pirms atbildēt uz jautājumu, ka tas ir izohorisks process, jums labāk jāiepazīst ideālās gāzes jēdziens. Fizikā ar to saprot jebkuru gāzi, kurā to veidojošo daļiņu vidējā kinētiskā enerģija ievērojami pārsniedz to mijiedarbības potenciālo enerģiju, un attālumi starp šīm daļiņām ir par vairākām kārtām lielāki par to lineārajiem izmēriem. Ievērojot norādītos nosacījumus, tas ir iespējams, veicotaprēķinos nav ņemta vērā mijiedarbības enerģija starp daļiņām (tā ir vienāda ar nulli), un var arī pieņemt, ka daļiņas ir materiāli punkti ar noteiktu masu m.
Vienīgais process, kas notiek ideālā gāzē, ir daļiņu sadursme ar vielu saturošā trauka sieniņām. Šīs sadursmes praksē izpaužas kā noteikta spiediena esamība gāzē P.
Parasti par ideālu gāzi ar pietiekamu precizitāti praktiskiem aprēķiniem var uzskatīt jebkuru gāzveida vielu, kas sastāv no relatīvi ķīmiski inertām molekulām un kurai ir zems spiediens un augsta temperatūra.
Vienādojums, kas apraksta ideālu gāzi
Protams, mēs runājam par universālo Klapeirona-Mendeļejeva likumu, kas būtu labi jāsaprot, lai saprastu, ka tas ir izohorisks process. Tātad universālajam stāvokļa vienādojumam ir šāda forma:
PV=nRT.
Tas ir, spiediena P un gāzes tilpuma V reizinājums ir vienāds ar absolūtās temperatūras T un vielas daudzuma molos n reizinājumu, kur R ir proporcionalitātes koeficients. Pašu vienādojumu 1834. gadā pirmo reizi pierakstīja Emīls Klepeirons, un 19. gadsimta 70. gados D. Mendeļejevs tajā aizvietoja vienas universālas gāzes konstantes R (8,314 J/(molK) konstantu vērtību kopu.)).
Saskaņā ar Klepeirona-Mendeļejeva vienādojumu slēgtā sistēmā gāzes daļiņu skaits paliek nemainīgs, tāpēc ir tikai trīs makroskopiski parametri, kas var mainīties (T, Pun V). Pēdējais fakts ir pamatā izpratnei par dažādiem izoprocesiem, kas tiks apspriesti turpmāk.
Kas ir izohorisks process?
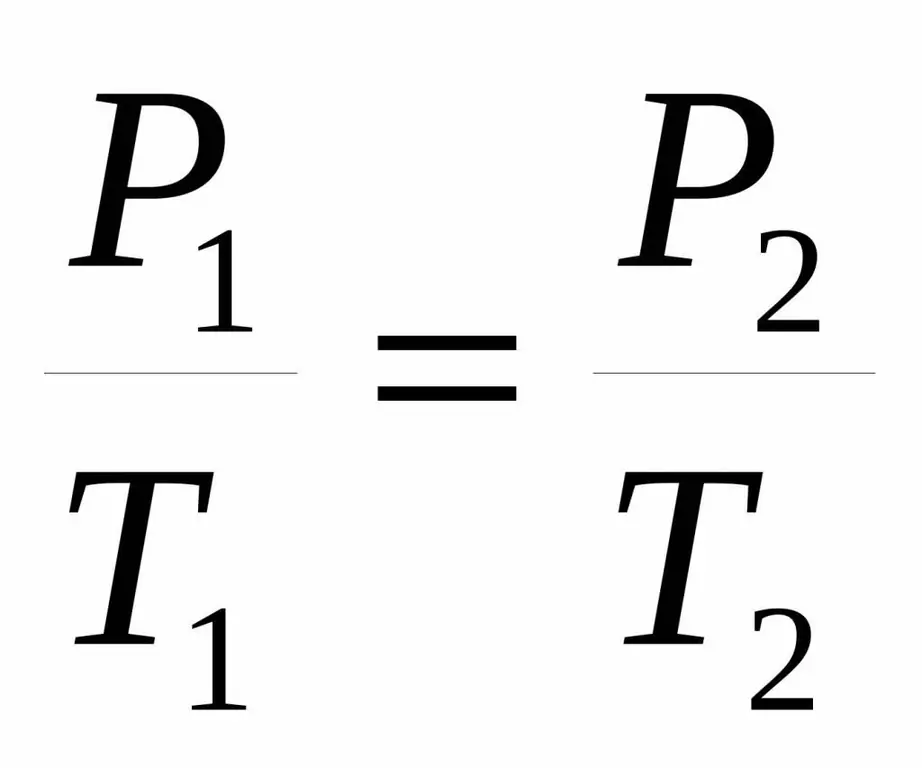
Ar šo procesu saprot absolūti jebkuras izmaiņas sistēmas stāvoklī, kurā tiek saglabāts tās apjoms.
Ja pievēršamies universālajam stāvokļa vienādojumam, var teikt, ka izohoriskā procesā gāzē mainās tikai spiediens un absolūtā temperatūra. Lai precīzi saprastu, kā mainās termodinamiskie parametri, mēs uzrakstām atbilstošo matemātisko izteiksmi:
P / T=konst.
Dažreiz šī vienlīdzība tiek dota nedaudz citā formā:
P1 / T1=P2 / T 2.
Abas vienādības tiek sauktas par Kārļa likumu pēc kāda franču zinātnieka vārda, kurš 18. gadsimta beigās eksperimentāli ieguva minēto atkarību.

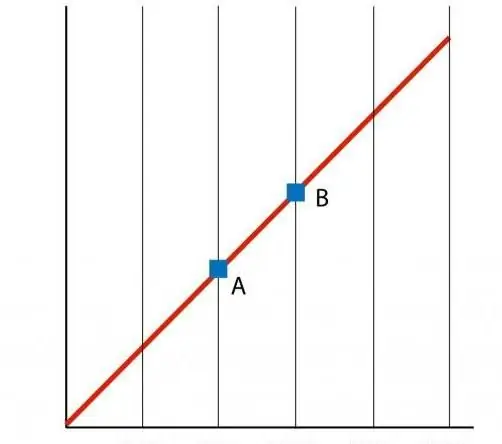
Ja veidojam funkcijas P(T) grafiku, tad iegūstam taisnās līnijas atkarību, ko sauc par izohoru. Jebkurš izohors (visām n un V vērtībām) ir taisna līnija.
Procesa enerģētiskais apraksts
Kā minēts, izohorisks process ir sistēmas stāvokļa maiņa, kas notiek slēgtā, bet ne izolētā sistēmā. Mēs runājam par siltuma apmaiņas iespēju starp gāzi un vidi. Kopumā jebkura siltuma Q padeve sistēmai rada divus rezultātus:
- maina iekšējo enerģiju U;
- gāzestrādā A, paplašinot vai slēdzot līgumus.
Pēdējais secinājums ir matemātiski uzrakstīts šādi:
Q=U + A.
Ideālas gāzes izohoriskais process pēc tās definīcijas nenozīmē gāzes veikto darbu, jo tās tilpums paliek nemainīgs. Tas nozīmē, ka viss sistēmai piegādātais siltums tiek izmantots, lai palielinātu tās iekšējo enerģiju:
Q=U.
Ja šajā izteiksmē aizstājam precīzo iekšējās enerģijas formulu, tad izohoriskā procesa siltumu var attēlot šādi:
Q=z / 2nRT.
Šeit z ir brīvības pakāpju skaits, ko nosaka gāzi veidojošo molekulu poliatomiskais raksturs. Monatomiskajai gāzei z=3, divatomu gāzei - 5, trīsatomu un vairāk - 6. Šeit ar brīvības pakāpēm mēs domājam translācijas un rotācijas pakāpes.
Ja salīdzinām gāzes sistēmas apkures efektivitāti izohoriskos un izobariskos procesos, tad pirmajā gadījumā iegūsim maksimālu efektivitāti, jo izobāriskās sistēmas stāvokļa maiņas laikā gāze izplešas un daļa siltuma padeves tiek tērēta darba veikšanai.
Izobarisks process
Iepriekš mēs sīki aprakstījām, ka tas ir izohorisks process. Tagad pateiksim dažus vārdus par citiem izoprocesiem. Sāksim ar izobariku. Pamatojoties uz nosaukumu, tas tiek saprasts kā sistēmas pāreja starp stāvokļiem nemainīgā spiedienā. Šis process ir aprakstīts Gay-Lussac likumā šādi:
V / T=konst.
Tāpat kā ar izohoru, arī V(T) izojosla attēlo taisnu līniju grafikā.
Parjebkura izobāriskā procesa gadījumā ir ērti aprēķināt gāzes veikto darbu, jo tas ir vienāds ar nemainīga spiediena un tilpuma izmaiņu reizinājumu.
Izotermisks process
Šis ir process, kurā sistēmas temperatūra paliek nemainīga. To apraksta Boila-Mariota likums ideālai gāzei. Interesanti atzīmēt, ka šis ir pirmais eksperimentāli atklātais gāzes likums (17. gadsimta otrajā pusē). Tā matemātiskais apzīmējums izskatās šādi:
PV=konst.
Izohoriskie un izotermiskie procesi atšķiras pēc to grafiskā attēlojuma, jo funkcija P(V) ir hiperboliska, nevis lineāra sakarība.
Problēmu risināšanas piemērs
Konsolidēsim rakstā sniegto teorētisko informāciju ar to pielietojumu praktiskas problēmas risināšanai. Ir zināms, ka tīrs gāzveida slāpeklis atradās cilindrā 1 atmosfēras spiedienā un 25 °C temperatūrā. Pēc gāzes balona uzkarsēšanas un spiediena mērīšanas tajā izrādījās 1,5 atmosfēras. Kāda ir gāzes temperatūra balonā pēc karsēšanas? Par cik daudz mainījās gāzes iekšējā enerģija, ja balonā bija 4 moli slāpekļa.
Lai atbildētu uz pirmo jautājumu, mēs izmantojam šādu izteicienu:
P1 / T1=P2 / T 2.
No kurienes mēs iegūstam:
T2=P2 / P1 T 1.
Šajā izteiksmē spiedienu var aizstāt ar patvaļīgām vienībāmmērījumi, jo tie sarūk, un temperatūra ir tikai kelvinos. To sakot, mēs iegūstam:
T2=1,5 /1298,15=447,224 K.
Aprēķinātā temperatūra Celsija grādos ir 174 °C.
Tā kā slāpekļa molekula ir divatomiska, tās iekšējās enerģijas izmaiņas karsēšanas laikā var noteikt šādi:
ΔU=5/2nRΔT.
Aizvietojot zināmās vērtības šajā izteiksmē, mēs iegūsim atbildi uz otro problēmas jautājumu: ΔU=+12,4 kJ.






