Vielas gāzveida agregāta stāvokļa termodinamika ir svarīga fizikas nozare, kas pēta termodinamisko līdzsvaru un kvazistatiskās pārejas sistēmās. Galvenais modelis, uz kura balstās sistēmu uzvedības prognozes, ir ideālās gāzes modelis. Izmantojot to, tika iegūts Mendeļejeva-Klapeirona vienādojums. Apsveriet to rakstā.
Ideāla gāze
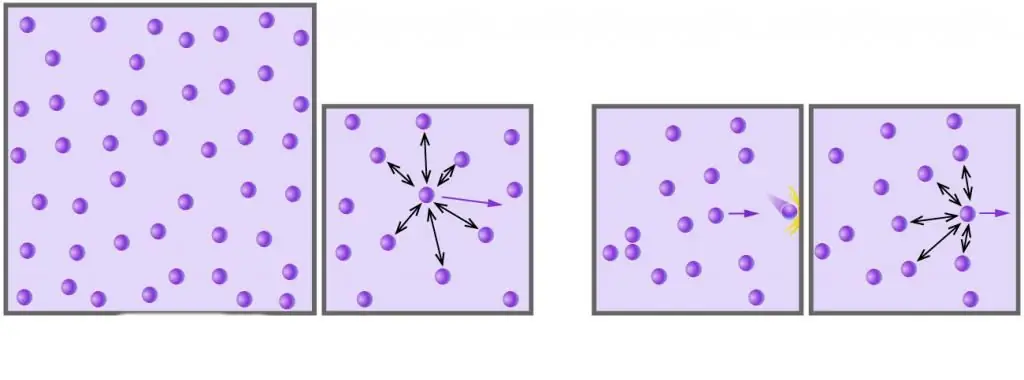
Kā jūs zināt, visas reālās gāzes sastāv no molekulām vai atomiem, kuru attālumi ir pārāk lieli salīdzinājumā ar to lielumu zemā spiedienā. Turklāt augstās temperatūrās absolūtā mērogā molekulu kinētiskā enerģija pārsniedz to potenciālo enerģiju, kas saistīta ar vāju dipola-dipola mijiedarbību (ja papildus šīm mijiedarbībām pastāv arī cita veida ķīmiskās saites, piemēram, jonu vai ūdeņradis, tad tie sniedz būtisku ieguldījumu iekšējās sistēmas enerģijas potenciālajā komponentē).
Sakarā arDaudzām reālām gāzēm normālos apstākļos var neņemt vērā to iekšējo mijiedarbību un daļiņu izmērus. Šie divi galvenie tuvinājumi veido ideālo gāzes modeli.
Mendeļejeva vienādojums fizikā

Pareizāk un godīgāk ir šo vienādojumu saukt par Klepeirona-Mendeļejeva likumu. Fakts ir tāds, ka to pirmo reizi ierakstīja franču inženieris Emīls Klepeirons 1834. gadā. Viņš to izdarīja, analizējot Boila-Mariotas, Geja-Lusaka un Čārlza gāzes likumus, kas atklāti 19. gadsimta sākumā.
Krievu ķīmiķa Dmitrija Mendeļejeva nopelns ir tajā, ka viņš piešķīra vienādojumam modernu un ērti lietojamu matemātisko formu. Jo īpaši Mendeļejevs vienādojumā ieviesa konstanti visām gāzēm R=8, 314 J/(molK). Pats Klepeirons izmantoja vairākas empīriskas konstantes, kas apgrūtina skaitļošanas procesu.
Mendeļejeva-Klepeirona vienādojums ir uzrakstīts šādi:
PV=nRT.
Šī vienādība nozīmē, ka spiediena P un tilpuma V reizinājums izteiksmes kreisajā pusē vienmēr ir proporcionāls absolūtās temperatūras T reizinājumam un vielas daudzumam n kreisajā pusē.
Pētītā izteiksme ļauj iegūt jebkuru gāzes likumu, ja labojat divus no četriem parametriem. Izoprocesu gadījumā tiek pētītas slēgtas sistēmas, kurās nenotiek vielu apmaiņa ar vidi (n=const). Šos procesus raksturo viens fiksēts termodinamiskais parametrs (T, P vai V).

Problēmas piemērs
Tagad atrisināsim Mendeļejeva-Klepeirona vienādojuma uzdevumu. Ir zināms, ka skābeklis, kas sver 500 gramus, atrodas cilindrā ar tilpumu 100 litri pie 2 atmosfēras spiediena. Kāda ir temperatūra balonā, ja sistēma atrodas termodinamiskā līdzsvarā.
Atgādināt, ka saskaņā ar definīciju vielas daudzumu aprēķina pēc formulas:
n=m/M.
Kur m ir visu sistēmas daļiņu masa, M ir to vidējā molārā masa. Šī vienādība ļauj pārrakstīt Mendeļejeva vienādojumu šādā formā:
PV=mRT/M.
Kur mēs iegūstam šī uzdevuma darba formulu:
T=PVM/(mR).
Atliek pārvērst visus daudzumus SI vienībās un aizstāt tos ar šo izteiksmi:
T=21013250, 10, 032/(0, 58, 314)=156 K.
Aprēķinātā temperatūra ir -117 oC. Lai gan skābeklis šajā temperatūrā joprojām ir gāzveida (tas kondensējas pie -182,96 oC), šādos apstākļos ideālās gāzes modeli var izmantot tikai, lai iegūtu aprēķinātās vērtības kvalitatīvu novērtējumu.






