No skolas mēs visi zinām likumu par paaugstināšanu pakāpē: jebkurš skaitlis ar eksponentu N ir vienāds ar rezultātu, reizinot šo skaitli ar sevi N reizes. Citiem vārdiem sakot, 7 līdz 3 pakāpei ir 7, kas reizināts ar sevi trīs reizes, tas ir, 343. Vēl viens noteikums ir tāds, ka, paaugstinot jebkuru vērtību līdz pakāpei 0, tiek iegūts viens, un negatīvas vērtības palielināšana ir parastas eksponēšanas rezultāts. ja tas ir pāra, un tas pats rezultāts ar mīnusa zīmi, ja tas ir nepāra.

Noteikumi sniedz arī atbildi par to, kā palielināt skaitli negatīvā pakāpē. Lai to izdarītu, jums parastajā veidā jāpalielina vajadzīgā vērtība par indikatora moduli un pēc tam jāsadala vienība ar rezultātu.
No šiem noteikumiem kļūst skaidrs, ka reālu uzdevumu izpildei ar lieliem apjomiem būs nepieciešama tehnisko līdzekļu pieejamība. Manuāli būs iespējams reizināt ar sevi maksimālo skaitļu diapazonu līdz divdesmit vai trīsdesmit un pēc tam ne vairāk kā trīs vai četras reizes. Nemaz nerunājot par to, ka tad arī dala vienību ar rezultātu. Tāpēc tiem, kam nav pie rokas īpašas inženierijaskalkulatoru, mēs parādīsim, kā programmā Excel palielināt skaitli ar negatīvu pakāpju.
Problēmu risināšana programmā Excel
Lai atrisinātu kāpināšanas problēmas, programmā Excel varat izmantot vienu no divām iespējām.
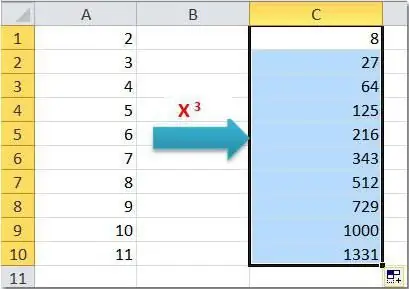
Pirmais ir formulas izmantošana ar standarta vāciņa simbolu. Ievadiet darblapas šūnās šādus datus:
| B | C | Formula | Rezultāts | |
| 2 | 7 | 3 | =B2^C2 | 343 |
Tādā pašā veidā jūs varat palielināt vēlamo vērtību līdz jebkurai pakāpei - negatīvai, daļējai. Rīkosimies šādi un atbildēsim uz jautājumu, kā pacelt skaitli negatīvā pakāpē. Piemērs:
| B | C | Formula | Rezultāts | |
| 2 | 7 | -3 | =B2^C2 | 0, 002915 |
Varat labot=B2^-C2 tieši formulā.
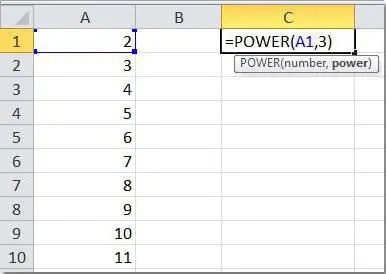
Otra iespēja ir izmantot gatavu funkciju "Grāds", kas aizņem divus obligātos argumentus - skaitli un rādītāju. Lai sāktu to lietot, pietiek ar “vienādības” zīmi (=) ievietot jebkurā brīvā šūnā,norādot uz formulas sākumu, un ievadiet iepriekš minētos vārdus. Atliek atlasīt divas šūnas, kas piedalīsies darbībā (vai manuāli norādīt konkrētus skaitļus), un nospiediet taustiņu Enter. Apskatīsim dažus vienkāršus piemērus.
| B | C | Formula | Rezultāts | ||
| 2 | 7 | 3 | =JAUDA(B2;C2) | 343 | |
| 3 | 7 | -3 | =JAUDA(B3;C3) |
|
Kā redzat, nav nekā sarežģīta, kā, izmantojot programmu Excel, palielināt skaitli līdz negatīvam un līdz normālam pakāpim. Galu galā, lai atrisinātu šo problēmu, varat izmantot gan pazīstamo “vāka” simbolu, gan viegli iegaumējamo programmas iebūvēto funkciju. Tas ir neapšaubāms pluss!
Pāriesim pie sarežģītākiem piemēriem. Atcerēsimies noteikumu par to, kā palielināt skaitli līdz daļskaitļa rakstzīmes negatīvam pakāpēm, un mēs redzēsim, ka šo uzdevumu programmā Excel ir ļoti viegli atrisināt.
Daļskaitļi
Īsi sakot, algoritms skaitļa aprēķināšanai ar daļskaitļu eksponentu ir šāds.
- Pārvērst daļskaitli par pareizu vai nepareizu daļskaitli.
- Palieliniet mūsu skaitli līdz iegūtās konvertētās daļskaitļa skaitītājam.
- No iepriekšējā rindkopā iegūtā skaitļa aprēķiniet sakni ar nosacījumu, ka saknes eksponentsbūs pirmajā posmā iegūtās daļas saucējs.
Piekrītiet, ka pat strādājot ar maziem skaitļiem un pareizām daļskaitļiem, šādi aprēķini var aizņemt daudz laika. Labi, ka izklājlapu procesoram Excel ir vienalga, kādu skaitli un kādā pakāpē celt. Mēģiniet Excel darblapā atrisināt šādu piemēru:
| B (skaitlis) | C | Konvertēt uz daļskaitli | Formula | Rezultāts | |
| 2 | 7 | 0, 4 | 2/5 | =JAUDA(B2;C2) | 2, 177906424 |
Izmantojot iepriekš minētos noteikumus, varat pārbaudīt un pārliecināties, vai aprēķins ir pareizs.
Mūsu raksta beigās tabulas veidā ar formulām un rezultātiem mēs sniegsim vairākus piemērus, kā palielināt skaitli negatīvā pakāpē, kā arī vairākus piemērus ar daļskaitļiem un pakāpēm.
Tabulas paraugs
Pārbaudiet tālāk norādītos piemērus Excel darblapā. Lai viss darbotos pareizi, kopējot formulu ir jāizmanto jaukta atsauce. Labojiet kolonnas numuru, kurā ir paceļamais skaitlis, un rindas numuru, kurā ir rādītājs. Jūsu formulai vajadzētu izskatīties apmēram šādi: "=$B4^C$3".
| Numurs/grāds | 1 | 2 | 3 | 0, 5 | -0, 5 |
| 1 | 1 | 1 | 1 | 1 | 1 |
| 2 | 2 | 4 | 8 | 1, 414214 | 0, 707107 |
| 7 | 7 | 49 | 343 | 2, 645751 | 0, 377964 |
| -7 | -7 | 49 | -343 | NUMBER! | NUMBER! |
| 0, 2 | 0, 2 | 0, 04 | 0, 008 | 0, 447214 | 2, 236068 |
| 0, 4 | 0, 4 | 0, 16 | 0, 064 | 0, 632456 |
1, 581139 |
| -0, 4 | -0, 4 | 0, 16 | -0, 064 | NUMBER! | NUMBER! |
Lūdzu, ņemiet vērā, ka pozitīvie skaitļi (pat tādi, kas nav veseli skaitļi) tiek aprēķināti bez problēmām nevienam eksponentam. Nav nekādu problēmu ar skaitļu palielināšanu līdz veseliem skaitļiem. Bet negatīva skaitļa paaugstināšana līdz daļējai pakāpei jums kļūs par kļūdu, jo nav iespējams ievērot norādīto noteikumumūsu raksta sākumā par negatīvu skaitļu konstruēšanu, jo paritāte ir tikai VESELS skaitļa raksturlielums.






