Termodinamikā, pētot pārejas no sistēmas sākotnējā stāvokļa uz gala stāvokli, ir svarīgi zināt procesa termisko efektu. Siltuma jaudas jēdziens ir cieši saistīts ar šo efektu. Šajā rakstā mēs apskatīsim jautājumu par to, ko nozīmē gāzes izohoriskā siltumietilpība.
Ideāla gāze
Ideāla gāze ir gāze, kuras daļiņas tiek uzskatītas par materiāliem punktiem, tas ir, tām nav izmēri, bet ir masa, un kurā visa iekšējā enerģija sastāv tikai no molekulu kustības kinētiskās enerģijas un atomi.
Jebkura īsta gāze ideālā gadījumā nekad neapmierinās aprakstīto modeli, jo tās daļiņām joprojām ir daži lineāri izmēri un tās mijiedarbojas viena ar otru, izmantojot vājas van der Vālsa saites vai cita veida ķīmiskās saites. Tomēr zemā spiedienā un augstā temperatūrā attālumi starp molekulām ir lieli, un to kinētiskā enerģija desmitiem reižu pārsniedz potenciālo enerģiju. Tas viss ļauj ar augstu precizitātes pakāpi piemērot ideālu modeli īstām gāzēm.
Gāzes iekšējā enerģija
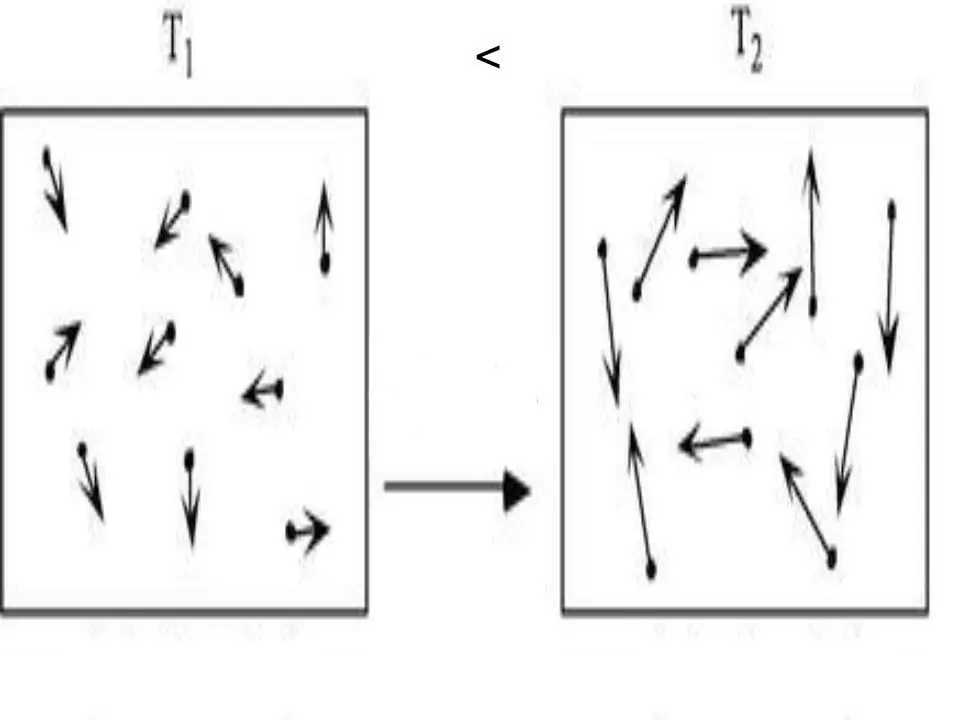
Jebkuras sistēmas iekšējā enerģija ir fizikāls raksturlielums, kas ir vienāds ar potenciālās un kinētiskās enerģijas summu. Tā kā ideālajās gāzēs potenciālo enerģiju var neņemt vērā, mēs varam uzrakstīt tām vienādību:
U=Ek.
Kur Ek ir kinētiskās sistēmas enerģija. Izmantojot molekulāri kinētisko teoriju un pielietojot universālo Klapeirona-Mendeļejeva stāvokļa vienādojumu, nav grūti iegūt U izteiksmi. Tas ir rakstīts zemāk:
U=z/2nRT.
Šeit T, R un n ir attiecīgi absolūtā temperatūra, gāzes konstante un vielas daudzums. Z vērtība ir vesels skaitlis, kas norāda gāzes molekulas brīvības pakāpju skaitu.
Izobariskā un izohoriskā siltumietilpība
Fizikā siltumietilpība ir siltuma daudzums, kas jāpiegādā pētāmajai sistēmai, lai to uzsildītu par vienu kelvinu. Pareiza ir arī apgrieztā definīcija, proti, siltuma jauda ir siltuma daudzums, ko sistēma atbrīvo, atdzesējot par vienu kelvinu.
Vienkāršākais veids sistēmai ir noteikt izohorisko siltuma jaudu. To saprot kā siltuma jaudu nemainīgā tilpumā. Tā kā sistēma šādos apstākļos neveic darbu, visa enerģija tiek tērēta iekšējo enerģijas rezervju palielināšanai. Izohorisko siltumietilpību apzīmēsim ar simbolu CV, tad varam rakstīt:
dU=CVdT.
Tas ir, iekšējās enerģijas izmaiņassistēma ir tieši proporcionāla tās temperatūras izmaiņām. Ja salīdzinām šo izteiksmi ar vienādību, kas rakstīta iepriekšējā rindkopā, tad ideālā gāzē nonākam pie formulas CV:
СV=z/2nR.
Šo vērtību ir neērti lietot praksē, jo tā ir atkarīga no vielas daudzuma sistēmā. Tāpēc tika ieviests īpatnējās izohoriskās siltumietilpības jēdziens, tas ir, vērtība, kas tiek aprēķināta vai nu uz 1 molu gāzes, vai uz 1 kg. Pirmo vērtību apzīmēsim ar simbolu CV, otro - ar simbolu CV m. Viņiem varat uzrakstīt šādas formulas:
CV=z/2R;
CVm=z/2R/M.
Šeit M ir molārā masa.
Izobariskais ir siltuma jauda, vienlaikus saglabājot nemainīgu spiedienu sistēmā. Šāda procesa piemērs ir gāzes izplešanās cilindrā zem virzuļa, kad tas tiek uzkarsēts. Atšķirībā no izohoriskā procesa izobāriskā procesa laikā sistēmai piegādātais siltums tiek tērēts iekšējās enerģijas palielināšanai un mehāniskā darba veikšanai, tas ir:
H=dU + PdV.
Izobāriskā procesa entalpija ir izobāriskās siltumietilpības un temperatūras izmaiņu reizinājums sistēmā, tas ir:
H=CPdT.
Ja ņemam vērā izplešanos pie nemainīga 1 mola gāzes spiediena, tad pirmais termodinamikas likums tiks uzrakstīts šādi:
CPdT=CV dT + RdT.
Pēdējais termins tiek iegūts no vienādojumaKlepeirons-Mendeļejevs. No šīs vienlīdzības izriet attiecība starp izobarisko un izohorisko siltuma jaudu:
CP=CV + R.
Ideālai gāzei īpatnējā molārā siltumietilpība nemainīgā spiedienā vienmēr ir lielāka par attiecīgo izohorisko raksturlielumu ar R=8, 314 J/(molK).
Molekulu brīvības pakāpes un siltumietilpība
Uzrakstīsim vēlreiz formulu konkrētajai molārajai izohoriskajai siltumietilpībai:
CV=z/2R.
Monatomiskas gāzes gadījumā vērtība z=3, jo atomi telpā var kustēties tikai trīs neatkarīgos virzienos.
Ja mēs runājam par gāzi, kas sastāv no diatomiskām molekulām, piemēram, skābekļa O2 vai ūdeņraža H2, tad, papildus translācijas kustībai šīs molekulas joprojām var griezties ap divām savstarpēji perpendikulārām asīm, tas ir, z būs vienāds ar 5.
Sarežģītākām molekulām izmantojiet z=6., lai noteiktu CV






