Lai uz papīra varētu attēlot objektus, kuriem patiesībā nav īpaši “ērti” izmēri, cilvēki izdomāja mērogu. Faktiski tas izskaidro, kam skala ir paredzēta.
Kad skolas mācību programma sāk atklāt mēroga jēdzienu
Pirmo reizi bērni saskaras ar šo vārdu, pētot teritorijas kartes un plānus. Skolotājs, kā piemēru izmantojot atlantus, skaidro, kāpēc skala ir vajadzīga, ko tā parāda. Tiek paskaidrots, ka jebkurš ģeogrāfisks objekts ir tik liels, ka būtu grūti un neērti to attēlot pilnā izmērā.
Cilvēki zīmēja reljefu samazinātā formā, taču šim nolūkam viņi neizmantoja nekādas precīzas attiecības. Tagad tas tiek darīts gudrāk - katrai kartē attēlotajai domuzīmei un līnijai ir izmērs, ko var reizināt ar noteiktu skaitli un uzzināt patieso garumu un platumu.
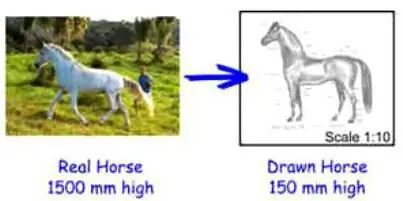
Ieraksta skala: pirmais veids, kā lasīt
Mērogu norāda ar diviem cipariem, kas atdalīti ar kolu. Pirmais cipars norāda izmēra vienības attēlā, otraisnorāda, cik reālo vienību attēlā atbilst pirmajam skaitlim. Piemēram, ja uz kāda plāna ir norādīts mērogs 1:1000 un izmēru vienības ir norādītas centimetros, tad viens centimetrs attēlā atbilst 1000 cm patiesībā. Tātad, kam tas mērogs ir paredzēts? Ar tās palīdzību jūs varat ne tikai samazināt noteiktus objektus grafiskajā plānā, bet arī precīzi aprēķināt to reālo izmēru.
Otrs skalas ierakstīšanas veids: kas ir ērti?
Iepriekšējo metodi skalas rakstīšanai caur kolu sauc par skaitlisko. Bet ir arī nosaukta skala. Viņa rekords ir šāds: 1 cm - 20 km. Izrādās, ka tādā veidā iespējams kompakti pierakstīt milzīgas skalas, kuras neizteiks ar cipariem ar vairākām nullēm, ja ir radusies situācija, kad vienā centimetrā nepieciešams norādīt vairākus simtus kilometru. Tajā pašā laikā uzreiz ir skaidrs, cik, ko un kādā. Šis ieraksts ir intuitīvāks un skaidrāks.
Mērogošana zīmēšanā: kas papildina iepriekš pētīto koncepciju
Mēroga jēdziens sastopams ne tikai ģeogrāfijā, bet arī tāda mācību priekšmeta kā zīmēšana apgūšanā. Tie paši principi tiek izmantoti dažādu objektu attēlošanai. Taču ir būtiska atšķirība: šeit priekšstatu par to, kam mērogs ir paredzēts, paplašina arī tas, ka ar to var attēlot mazas detaļas lielākā mērogā. Ģeogrāfijā mēs par to nerunājam, jo ģeogrāfijā nav tik mazu objektu, lai būtu nepieciešams tos palielināt. Kontinenti un kalni, upes un ezeri jebkurā gadījumā ir lielāki par A4 papīra loksnēm vai patA1.
Studējot zīmējumu, varat izmantot mērogu, lai lielākā veidā attēlotu mazākās detaļas, piemēram, skrūvi vai zobratu.
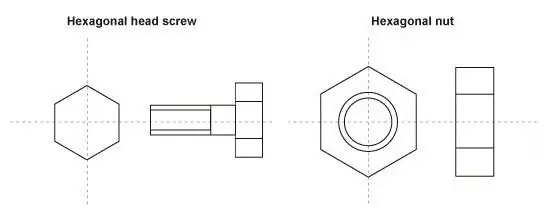
Tātad, kāpēc mums šajā gadījumā ir vajadzīgi svari? Ar tās palīdzību jūs varat ērtāk, skaidrāk un detalizētāk attēlot nelielu elementu. Šajā gadījumā apzīmējumā notiek otrādi: pirmais skaitlis būs lielāks par otro, un apzīmējums 100:1 skanēs apmēram šādi: 100 attēla metriskās vienības atbilst vienai faktiskā izmēra vienībai.
Daži precizējoši piemēri
Kam ir mērogs, ko tas parāda mazāka objekta attēla gadījumā, kas ir rezultāts uz papīra? Atkal mums ir precīza detaļas attēla un reālā objekta izmēru attiecība. Atcerieties to pašu mērogu 100:1. Izrādās, ka simts milimetros attēlā ir tikai viens milimetrs reālā izmēra. Ja attēlā daļa ir 500 milimetrus plata, tās faktiskais platums ir tikai 5 milimetri.
Ja atceramies pirmo gadījumu, attēls uz liela objekta mazākas kopijas lapas, mērogs 1:100 nozīmēs, ka viens milimetrs attēlā satur 100 milimetrus patiesā izmēra. Tātad, ja objekts zīmējumā vai kartē ir 80 milimetrus garš, objekta faktiskais garums būs 8000 milimetri. Skaidrs piemērs tam, kam ir mērogs un kāds ir ērts cilvēces izgudrojums.
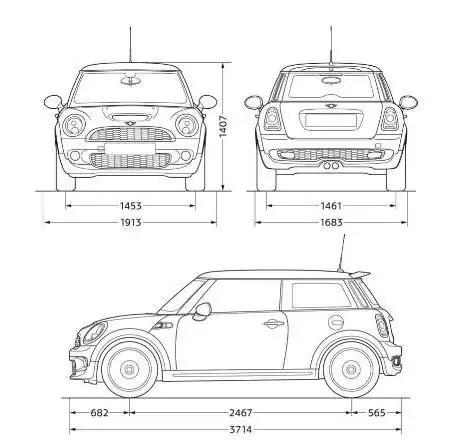
Svaru lietošanā galvenais ir nekavējotiesatcerieties, ka pirmais cipars attiecas uz attēlu, bet otrais uz objektu faktisko izmēru. Lai turpmāk neapjuktu, lai šos pamatus nostiprinātu, skolās notiek praktiskās nodarbības ģeogrāfijā, lai bērni vairākas reizes, izmantojot atlantu, skaidrotu un aprēķinātu reālo objektu izmērus. Tas pats notiek zīmēšanas stundās.
Apkopojiet
Kam paredzēta skala? Atbilde uz šo jautājumu sastāv no trim punktiem, kas jums vienkārši jāatceras:
- Pirmkārt - mērogs ir nepieciešams lielu objektu attēlošanai uz apskatei ērtas virsmas.
- Otrais - mērogs ir nepieciešams, lai mazus objektus attēlotu lielākā izmērā.
- Treškārt - mērogs ir nepieciešams, lai varētu precīzi noteikt reāla objekta izmēru neatkarīgi no tā sākotnējā izmēra, maza vai liela.






