Viens no galvenajiem dinamisko vadības sistēmu analīzes uzdevumiem ir to stabilitātes problēmas risinājums. To stabilitāte ir viena no svarīgākajām vadības koncepcijas īpašībām. Sistēma tiek uzskatīta par nestabilu, ja tā neatgriežas sākotnējā stāvoklī, bet turpina svārstīties pēc tam, kad ir veiktas dažas izmaiņas ieejā vai ir nevēlamu traucējumu ietekmē.
Galvenā jēdziena definīcija
Saskaņā ar sistēmas stabilitātes jēdzienu tās līdzsvara stāvoklis ir saistīts ar to, ka uz to nav traucējošu faktoru ietekmes. Šajā situācijā starpība starp iestatīto un faktisko stāvokli mēdz būt nulle. Stabilitāte ir tās spēja atgriezties sākotnējā līdzsvara stāvoklī pēc tam, kad ir beigusies perturbācija, kas izraisīja tā pārkāpumu. Nestabila sistēma traucējuma ietekmes dēļ attālinās no līdzsvara stāvokļa vai svārstās, kuras amplitūda pakāpeniskipieaug.

Stabilitātes apstākļi
Lai nodrošinātu sistēmas stabilitāti ar nemainīgu laiku, ir jāievēro šādi divi nosacījumi:
- Viņa izveidos ierobežotu izvadi katrai ievadei; ja nav ievades, izvadei jābūt nullei neatkarīgi no sākotnējiem nosacījumiem.
- Sistēmas stabilitāti var saukt par absolūto vai relatīvo stabilitāti. Iesniegtais termins tiek lietots saistībā ar pētījumu, kurā tiek salīdzināti noteikti daudzumi, to darbības apstākļi. Stabilitāte ir gala rezultāts, ko rada rezultāts.
Ja sistēmas izvade ir bezgalīga, pat ja tai tiek lietota ierobežota ievade, tad tā tiks uzskatīta par nestabilu, t.i., pēc savas būtības stabila, tai ir ierobežots izbeigums, kad sistēmai tiek lietots ierobežots sākums. pati.
Šajā gadījumā ar ievadi saprot dažādus ārējās vides ietekmes uz sistēmu pielietojuma punktus. Izvade ir tās darbības galaprodukts, kas ir pārveidoto ievaddatu veidā.
Nepārtrauktā lineārā laika sistēmā stabilitātes nosacījumu var uzrakstīt konkrētai impulsa reakcijai.
Ja tas ir diskrēts, stabilitātes indeksu var uzrakstīt arī konkrētai impulsa reakcijai.
Nestabilā stāvoklī gan nepārtrauktās, gan ierobežotās sistēmās šīs izteiksmes būs bezgalīgas.
Stabilitātes un traucējumu veidi
Zem statiskāAr sistēmas stabilitāti saprot tās spēju pēc nelielas perturbācijas nodrošināt sākotnējā (vai tuvu sākotnējam) režīma atjaunošanu. Saskaņā ar šajā kontekstā piedāvāto jēdzienu viņi ņem vērā svārstības, kas ietekmē tā uzvedību neatkarīgi no tā, kur parādās pieaugums vai kritums un kāds ir to lielums. Pamatojoties uz to, šie režīmi, kas ir tuvi sākotnējam, ļauj to uzskatīt par lineāru.
Sistēmu dinamiskā stabilitāte ir to spēja atjaunot sākotnējo stāvokli pēc lieliem traucējumiem.
Ar lielām svārstībām tiek saprasta tāda kustība, kuras ietekmes raksturs un tai atbilstošā uzvedība nosaka pastāvēšanas laiku, lielumu un rašanās vietu.
Pamatojoties uz to, sistēma šajā diapazonā ir definēta kā nelineāra.
Ilgtspējības noteikšanas kritēriji
Galvenais lineāras sistēmas stabilitātes nosacījums ir nevis traucējumu raksturs, bet gan tās struktūra. Tiek uzskatīts, ka šī stabilitāte "mazajā" tiek noteikta, ja tās robežas nav noteiktas. Stabilitāti "lielajā" nosaka robežas un reālo noviržu atbilstība šīm noteiktajām robežām.
Lai noteiktu sistēmas stabilitāti, tiek izmantoti šādi kritēriji:
- saknes kritērijs;
- Stodolas kritērijs;
- Hurvica kritērijs;
- Nikvista kritērijs;
- Mihailova kritērijs un citi
Atsevišķu saišu stabilitātes noteikšanai tiek izmantots saknes kritērijs un Stodola vērtēšanas tehnikaun atvērtās sistēmas. Hurvica kritērijs ir algebrisks un ļauj bez kavēšanās noteikt slēgtu sistēmu stabilitāti. Nyquist un Mihailov kritēriji ir biežuma kritēriji. Tos izmanto, lai noteiktu slēgtu sistēmu stabilitāti, pamatojoties uz to frekvences reakciju.

Sākotnējais kritērijs
Tas ļauj noteikt sistēmas stabilitāti, pamatojoties uz pārsūtīšanas funkcijas formu. Tās uzvedības īpašības raksturo raksturīgs polinoms (pārsūtīšanas funkcijas saucējs). Ja saucēju pielīdzināsim nullei, iegūtā vienādojuma saknes ļaus noteikt stabilitātes pakāpi.
Saskaņā ar šo kritēriju lineārā sistēma būs stabila, ja visas vienādojuma saknes atrodas kreisajā pusplaknē. Ja vismaz viens no tiem atrodas uz stabilitātes robežas, tas arī būs pie robežas. Ja vismaz viens no tiem atrodas labajā pusplaknē, sistēmu var uzskatīt par nestabilu.
Stodolas kritērijs
Tas izriet no saknes definīcijas. Saskaņā ar Stodola kritēriju lineāro sistēmu var uzskatīt par stabilu, ja visi polinoma koeficienti ir pozitīvi.
Hurvica kritērijs
Šis kritērijs tiek izmantots slēgtas sistēmas raksturīgajam polinomam. Saskaņā ar šo paņēmienu pietiekams stabilitātes nosacījums ir tas, ka determinanta un visu matricas galveno diagonālo minoru vērtība ir lielāka par nulli. Ja vismaz viens no tiem ir vienādsnulle, tas tiek uzskatīts par stabilitātes robežu. Ja ir vismaz viens negatīvs determinants, tas jāuzskata par nestabilu.
Nikvista kritērijs
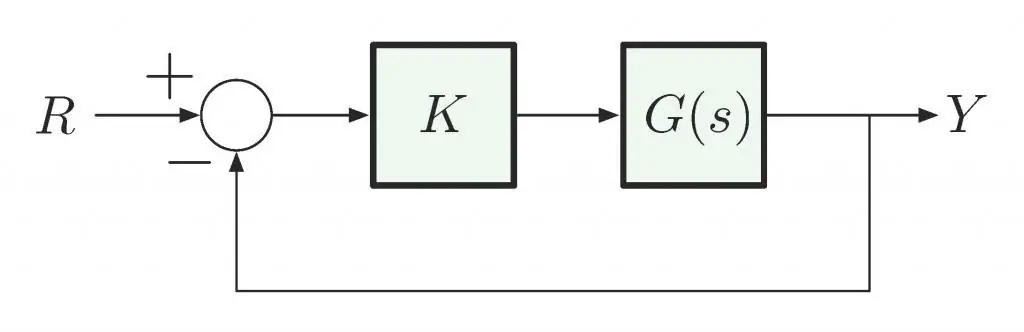
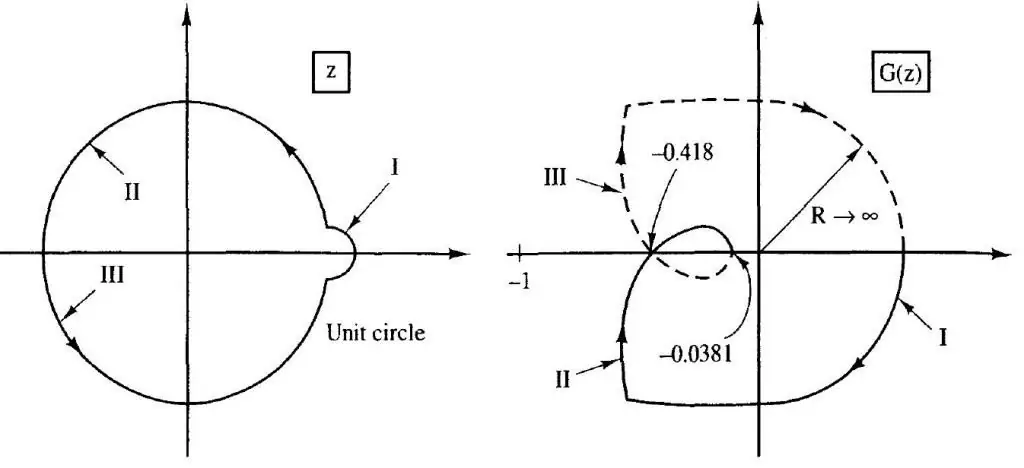
Šīs metodes pamatā ir līknes izveidošana, kas savieno mainīgā lieluma vektora galus, kas parāda pārsūtīšanas funkciju. Kritērija formulējums ir šāds: slēgta sistēma tiek uzskatīta par stabilu, ja funkcijas līkne neiekļauj punktu ar koordinātām (-1, j0) kompleksajā plaknē.
Finanšu stabilitātes sistēma
Finanšu noturība ir stāvoklis, kurā sistēma, t.i., galvenie tirgi un institūcijas, ir noturīga pret ekonomiskiem satricinājumiem un ir gatava nevainojami veikt savas pamatfunkcijas - naudas plūsmas starpniecību, riska pārvaldību un maksājumu kārtību.
Tā kā interpretācijas nodrošināšanai ir savstarpējās atkarības attiecības (gan vertikāli, gan horizontāli), analīzei jāaptver visa finanšu starpniecības sistēma. Citiem vārdiem sakot, papildus banku sektoram ir jāanalizē arī nebanku institūcijas, kas tādā vai citādā veidā ir iesaistītas starpniecībā. Tie ietver daudzu veidu iestādes, tostarp brokeru sabiedrības, ieguldījumu fondus, apdrošinātājus un citas (dažādas) struktūras. Analizējot finanšu stabilitātes sistēmu, tiek pētīts, cik lielā mērā visa struktūra spēj izturēt ārējos un iekšējos satricinājumus. Protams, ne vienmēr krīzes noved pie satricinājumiem, bet gan pati nestabilā finanšu videpati par sevi var kavēt veselīgu ekonomikas attīstību.
Finansiālās nestabilitātes cēloņus nosaka dažādas teorijas. To nozīme var atšķirties atkarībā no perioda un analīzē iesaistītajām valstīm. Starp problemātiskajiem faktoriem, kas ietekmē visu finanšu sistēmu, literatūrā parasti ir norādīts:
- straujā finanšu sektora liberalizācija;
- neadekvāta ekonomiskā politika;
- Nemērķēta valūtas maiņas kursa mehānisms;
- neefektīva resursu sadale;
- vāja pārraudzība;
- Nepietiekams grāmatvedības un audita regulējums.
Iespējamie cēloņi parādās ne tikai kolektīvi, bet arī individuāli vai nejaušā kombinācijā, tāpēc finanšu stabilitātes analīze ir ārkārtīgi grūts uzdevums. Koncentrēšanās uz atsevišķām nozarēm izkropļo kopējo ainu, tāpēc, pētot finanšu stabilitāti, jautājumi ir jāaplūko to sarežģītībā.

Uzņēmuma sistēmas stabilitātes analīzes process notiek vairākos posmos.
Sākotnēji tiek izvērtēti un analizēti absolūtie un relatīvie finanšu stabilitātes rādītāji. Otrajā posmā faktori tiek sadalīti atbilstoši to nozīmīgumam, tiek kvalitatīvi un kvantitatīvi novērtēta to ietekme.
Uzņēmumu finansiālā spēka rādītāji
Uzņēmuma finansiālais stāvoklis, tā stabilitāte lielā mērā ir atkarīga no optimālās kapitāla avotu struktūras, tas ir, parāda attiecības pret pašu resursiem, no optimālāuzņēmuma aktīvu struktūru un, pirmkārt, par pamatlīdzekļu un apgrozāmo līdzekļu attiecību, kā arī uzņēmuma līdzekļu un saistību atlikumu.
Tāpēc ir svarīgi izpētīt riska kapitāla avotu struktūru un novērtēt finanšu stabilitātes un riska pakāpi. Šim nolūkam tiek izmantoti sistēmas stabilitātes koeficienti:
- autonomijas (neatkarības) koeficients - kapitāla daļa bilancē;
- atkarības rādītājs - aizņemtā kapitāla daļa bilancē;
- tekošā parāda rādītājs - īstermiņa finanšu saistību attiecība pret bilanci;
- finanšu stabilitātes rādītājs (ilgtermiņa finansiālā neatkarība) - kapitāla un ilgtermiņa parāda attiecība pret bilanci;
- parādu segšanas koeficients (maksātspējas rādītājs) - kapitāla attiecība pret parādu;
- finanšu sviras rādītājs (finanšu riska rādītājs) - parāda attiecība pret kapitālu.

Jo augstāks ir tādu rādītāju līmenis kā autonomija, finanšu stabilitāte, parāda kapitāla segums, jo zemāks ir citas koeficientu grupas līmenis (atkarība, pašreizējais parāds, ilgtermiņa saistības pret investoriem) un attiecīgi uzņēmuma finansiālā stāvokļa stabilitāte. Finanšu sviras tiek sauktas arī par finanšu svirām.






